Optimizing KataGo Performance with CMA-ES Parameter Tuning
Welcome to my personal exploration of parameter tuning for KataGo, a Go/Baduk/Weiqi playing AI. In this blog post, I’ll share my experiments with different configurations and parameters in an attempt to optimize the performance of KataGo.
To do this, I used Covariance Matrix Adaptation Evolution Strategy (CMA-ES), an evolutionary algorithm for difficult non-linear non-convex black-box optimization problems. With a set game configuration, I defined the parameter search ranges and CMA-ES configurations, and then evaluated the solutions. I’ll share the results of the CMA-ES convergence graph, comparison of default and CMA-ES KataGo parameters, and a strength difference analysis. The source code for my experiment is also provided for those who wish to delve deeper.
Game Configurations
- 9x9 board
"maxVisits": 16
Parameter Search Ranges
0: 0 < cpuctExploration < 4.01: 0 < cpuctExplorationLog < 1.802: 0 < winLossUtilityFactor < 1.03: 0 < staticScoreUtilityFactor < 1.04: 0 < dynamicScoreUtilityFactor < 1.0
CMA-ES Configurations
- Population size is set to 50.
- Maximum number of function evaluations is set to 4096.
CMA-ES Solutions Evaluation
- Match 1 game to compare two solutions.
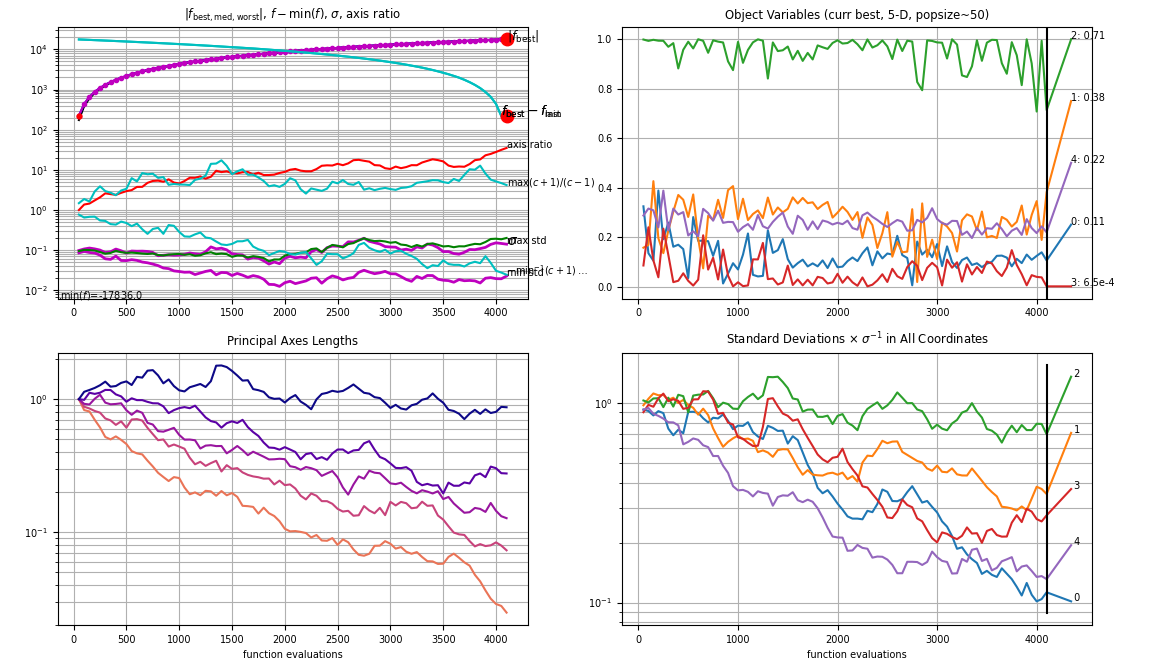
CMA-ES Convergence Graph
(25_w,50)-aCMA-ES (mu_w=14.0,w_1=14%) in dimension 5 (seed=525441, Thu Jul 27 20:48:58 2023)
Iterat #Fevals function value axis ratio sigma min&max std t[m:s]
1 50 -2.230000000000000e+02 1.0e+00 9.54e-02 9e-02 1e-01 24:52.6
2 100 -4.380000000000000e+02 1.4e+00 1.02e-01 9e-02 1e-01 71:53.6
3 150 -6.560000000000000e+02 1.5e+00 1.01e-01 9e-02 1e-01 95:51.8
4 200 -8.790000000000000e+02 1.7e+00 9.85e-02 9e-02 1e-01 120:48.5
5 250 -1.094000000000000e+03 2.1e+00 9.03e-02 8e-02 1e-01 144:44.9
6 300 -1.314000000000000e+03 2.6e+00 8.21e-02 6e-02 9e-02 169:07.6
7 350 -1.530000000000000e+03 2.5e+00 8.57e-02 6e-02 9e-02 193:16.0
8 400 -1.747000000000000e+03 2.4e+00 9.70e-02 7e-02 1e-01 217:24.5
9 450 -1.968000000000000e+03 2.7e+00 8.94e-02 6e-02 1e-01 241:54.0
10 500 -2.182000000000000e+03 3.0e+00 8.63e-02 6e-02 8e-02 265:49.1
11 550 -2.405000000000000e+03 3.1e+00 8.75e-02 6e-02 1e-01 290:37.2
12 600 -2.624000000000000e+03 3.8e+00 8.54e-02 6e-02 9e-02 315:02.6
13 650 -2.843000000000000e+03 3.8e+00 8.26e-02 5e-02 1e-01 339:17.8
14 700 -3.051000000000000e+03 4.8e+00 8.08e-02 5e-02 9e-02 362:15.2
15 750 -3.271000000000000e+03 5.3e+00 8.32e-02 5e-02 9e-02 386:38.8
16 800 -3.486000000000000e+03 5.4e+00 7.62e-02 4e-02 7e-02 410:33.5
17 850 -3.696000000000000e+03 5.1e+00 7.44e-02 4e-02 7e-02 433:48.9
18 900 -3.909000000000000e+03 5.8e+00 7.78e-02 3e-02 8e-02 457:13.1
19 950 -4.129000000000000e+03 4.8e+00 7.99e-02 3e-02 8e-02 481:28.3
20 1000 -4.341000000000000e+03 4.6e+00 8.09e-02 3e-02 8e-02 504:46.8
21 1050 -4.559000000000000e+03 5.3e+00 7.71e-02 3e-02 8e-02 528:41.3
22 1100 -4.777000000000000e+03 6.4e+00 7.96e-02 3e-02 9e-02 552:38.2
23 1150 -4.993000000000000e+03 6.4e+00 7.29e-02 2e-02 8e-02 576:45.1
24 1200 -5.207000000000000e+03 6.9e+00 7.50e-02 3e-02 8e-02 600:17.1
25 1250 -5.427000000000000e+03 6.0e+00 8.37e-02 3e-02 9e-02 624:17.1
26 1300 -5.640000000000000e+03 6.7e+00 8.93e-02 3e-02 1e-01 647:38.9
27 1350 -5.856000000000000e+03 9.5e+00 8.00e-02 2e-02 1e-01 671:17.6
28 1400 -6.078000000000000e+03 8.8e+00 8.27e-02 3e-02 1e-01 695:29.6
29 1450 -6.299000000000000e+03 9.2e+00 8.00e-02 3e-02 1e-01 719:52.1
30 1500 -6.520000000000000e+03 8.3e+00 6.85e-02 2e-02 8e-02 744:25.6
31 1550 -6.714000000000000e+03 8.2e+00 7.40e-02 3e-02 8e-02 765:57.8
32 1600 -6.918000000000000e+03 8.8e+00 7.35e-02 2e-02 8e-02 788:31.7
33 1650 -7.138000000000000e+03 8.9e+00 6.61e-02 2e-02 6e-02 812:48.4
34 1700 -7.328000000000000e+03 7.7e+00 7.12e-02 2e-02 7e-02 833:51.2
35 1750 -7.557000000000000e+03 8.5e+00 6.85e-02 2e-02 6e-02 858:56.0
36 1800 -7.783000000000000e+03 7.4e+00 6.39e-02 2e-02 5e-02 883:46.9
37 1850 -8.006000000000000e+03 7.5e+00 5.29e-02 1e-02 5e-02 908:25.4
38 1900 -8.229000000000000e+03 7.6e+00 5.89e-02 1e-02 5e-02 932:55.3
39 1950 -8.441000000000000e+03 8.4e+00 5.88e-02 1e-02 5e-02 956:12.9
40 2000 -8.661000000000000e+03 8.9e+00 7.33e-02 2e-02 6e-02 980:25.7
41 2050 -8.881000000000000e+03 1.0e+01 8.00e-02 2e-02 7e-02 1004:27.2
42 2100 -9.105000000000000e+03 1.1e+01 8.12e-02 1e-02 6e-02 1028:58.1
43 2150 -9.320000000000000e+03 9.6e+00 8.74e-02 2e-02 7e-02 1052:37.7
44 2200 -9.539000000000000e+03 9.2e+00 8.85e-02 2e-02 6e-02 1076:56.0
45 2250 -9.758000000000000e+03 9.2e+00 1.07e-01 2e-02 9e-02 1101:00.1
46 2300 -9.968000000000000e+03 1.0e+01 1.11e-01 2e-02 1e-01 1124:15.2
47 2350 -1.018700000000000e+04 1.3e+01 9.00e-02 2e-02 9e-02 1148:33.2
48 2400 -1.040700000000000e+04 1.3e+01 1.15e-01 2e-02 1e-01 1172:40.7
49 2450 -1.062800000000000e+04 1.3e+01 1.36e-01 2e-02 1e-01 1196:59.5
50 2500 -1.084400000000000e+04 1.4e+01 1.29e-01 2e-02 1e-01 1220:52.2
51 2550 -1.106900000000000e+04 1.3e+01 1.18e-01 2e-02 1e-01 1245:45.7
52 2600 -1.128300000000000e+04 1.4e+01 1.43e-01 2e-02 2e-01 1269:38.2
53 2650 -1.150400000000000e+04 1.7e+01 1.50e-01 2e-02 2e-01 1294:08.0
54 2700 -1.172200000000000e+04 1.8e+01 1.76e-01 3e-02 2e-01 1318:10.2
55 2750 -1.194100000000000e+04 1.7e+01 1.99e-01 3e-02 2e-01 1342:26.5
56 2800 -1.216300000000000e+04 1.6e+01 1.79e-01 3e-02 2e-01 1366:53.5
57 2850 -1.237700000000000e+04 1.3e+01 1.69e-01 3e-02 2e-01 1390:38.0
58 2900 -1.259500000000000e+04 1.3e+01 1.72e-01 3e-02 1e-01 1414:41.9
59 2950 -1.281700000000000e+04 1.1e+01 1.66e-01 3e-02 1e-01 1439:14.7
60 3000 -1.303300000000000e+04 1.1e+01 1.54e-01 3e-02 1e-01 1463:11.0
61 3050 -1.324400000000000e+04 1.2e+01 1.60e-01 3e-02 1e-01 1486:24.4
62 3100 -1.346500000000000e+04 1.1e+01 1.38e-01 2e-02 1e-01 1510:45.8
63 3150 -1.368800000000000e+04 1.2e+01 1.34e-01 2e-02 1e-01 1535:33.1
64 3200 -1.390800000000000e+04 1.3e+01 1.20e-01 2e-02 1e-01 1559:53.1
65 3250 -1.411900000000000e+04 1.3e+01 1.35e-01 2e-02 1e-01 1583:15.7
66 3300 -1.433500000000000e+04 1.5e+01 1.24e-01 2e-02 1e-01 1607:03.3
67 3350 -1.455900000000000e+04 1.7e+01 1.43e-01 2e-02 1e-01 1631:39.7
68 3400 -1.478000000000000e+04 1.8e+01 1.48e-01 2e-02 1e-01 1656:01.6
69 3450 -1.500400000000000e+04 1.8e+01 1.37e-01 2e-02 1e-01 1680:26.0
70 3500 -1.522500000000000e+04 1.6e+01 1.24e-01 2e-02 9e-02 1704:47.9
71 3550 -1.543600000000000e+04 1.3e+01 1.27e-01 2e-02 9e-02 1728:01.8
72 3600 -1.565300000000000e+04 1.2e+01 1.19e-01 2e-02 8e-02 1751:54.1
73 3650 -1.586300000000000e+04 1.2e+01 1.26e-01 2e-02 8e-02 1774:53.8
74 3700 -1.608900000000000e+04 1.2e+01 1.25e-01 2e-02 9e-02 1799:57.2
75 3750 -1.631100000000000e+04 1.4e+01 1.35e-01 2e-02 1e-01 1824:33.2
76 3800 -1.653300000000000e+04 1.7e+01 1.44e-01 2e-02 1e-01 1849:07.5
77 3850 -1.675100000000000e+04 1.8e+01 1.41e-01 2e-02 1e-01 1873:10.7
78 3900 -1.697000000000000e+04 2.3e+01 1.61e-01 2e-02 1e-01 1897:25.1
79 3950 -1.718000000000000e+04 2.5e+01 1.91e-01 2e-02 1e-01 1920:39.5
80 4000 -1.739700000000000e+04 2.8e+01 1.94e-01 2e-02 2e-01 1944:40.3
81 4050 -1.761700000000000e+04 3.1e+01 1.87e-01 2e-02 1e-01 1968:58.6
82 4100 -1.783600000000000e+04 3.5e+01 2.02e-01 2e-02 1e-01 1993:17.5
termination on maxfevals=4096 (Sat Jul 29 06:02:16 2023)
final/bestever f-value = -1.783600e+04 -1.783600e+04 after 4101/4097 evaluations
incumbent solution: [0.10899950093264148, 0.32887780262091476, 0.8099529685218856, 0.03984297292283672, 0.219613034476377]
std deviation: [0.022789306628414642, 0.07097373410740293, 0.141620148710783, 0.055441744647035475, 0.026523563086393906]
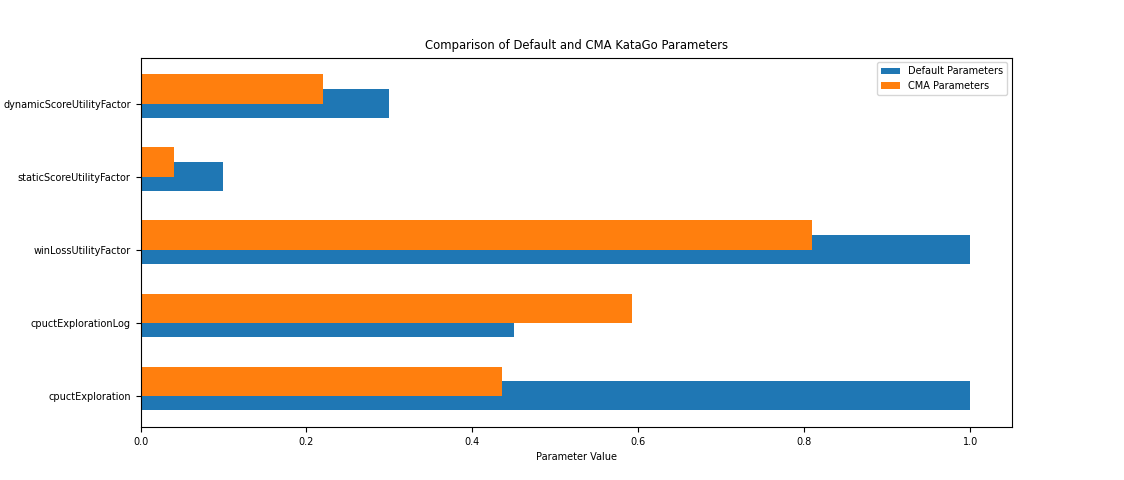
Comparison of Default and CMA-ES KataGo Parameters
=== Default KataGo parameters (start) ===
cpuctExploration: 1.0
cpuctExplorationLog: 0.45
winLossUtilityFactor: 1.0
staticScoreUtilityFactor: 0.1
dynamicScoreUtilityFactor: 0.3
=== Default KataGo parameters (end) ===
=== CMA KataGo parameters (start) ===
cpuctExploration: 0.4359980037305659
cpuctExplorationLog: 0.5919800447176465
winLossUtilityFactor: 0.8099529685218856
staticScoreUtilityFactor: 0.03984297292283672
dynamicScoreUtilityFactor: 0.219613034476377
=== CMA KataGo parameters (end) ===
Strength Difference between Default and CMA-ES KataGo Parameters
Verifying goodness of CMA KataGo command with 100 games...
Games: 100
Black:draw:white = 75:0:25
Default:CMA = 45:55
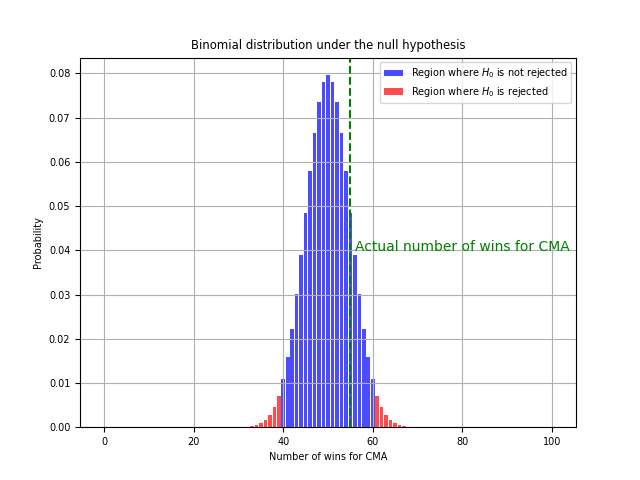
The actual number of wins for CMA is in the region where null hypothesis is not rejected with the significance level of 0.05.
Conclusion
In this blog post, I have demonstrated the process and results of using CMA-ES to optimize the parameters of KataGo, a Go-playing AI. My experiments resulted in a unique set of parameters that differ from the default KataGo parameters. When these were tested over 100 games, the new parameters showed a competitive performance compared to the default settings.
It’s important to note that, while the results are promising, the actual number of wins for CMA is within the region where the null hypothesis is not rejected with a significance level of 0.05. This means that although there is a difference, we cannot say with 95% confidence that the CMA parameters significantly improve the performance of KataGo.
As such, it’s clear that AI parameter tuning is a complex and nuanced process. While evolutionary algorithms like CMA-ES offer powerful tools for optimization, they require careful interpretation and analysis. It’s my hope that this deep dive into parameter tuning for KataGo has provided some valuable insights into this process.
Source Code
Here is the source code.